威胁情报质量评价和威胁情报商评价,一直是威胁情报界热门的话题,然而,如何对威胁情报逐条进行自定义分数设定,以及如何对情报商进行整体评价,能够参考的规则很少。笔者就此分享几个模型。为了简化模型,笔者进行了如下假设:
假设1:忽略了“少数派报告”的情形。包括:仅有少数或个别厂商提供了某情报(无论正确与否),或者少数厂商提供了正确情报。
假设2:对比维度已经标准化。为了能够对情报商进行客观的对比评价,需要注意情报商质量的计算维度应当进行统一,例如:对比信誉值或置信度时,需要注意其构成。A供应商仅对可能性进行了计算,而B供应商的结果中可能含有时间维度,两者进行对比可能无法产生预期效果。
假设3: 评估样本数量充足。评估结果基于统计数字,因此参与评估的样本数量必须充足,才能获得可信的评估结果。
假设4:未设置结果验证参数。针对情报,分析人员可以采用验证机制对情报内容进行有效性验证,通过验证结果评定情报的准确性、时效等因素,本文假设验证结果不影响情报评估。
(针对以上假设,需要进行模型修正。另外,文中模型在工程应用中需要采用收敛公式进行修正。有兴趣的同行,欢迎交流。)
评价模型如下:
1.平均值
基础模型采用平均值作为单条情报的质量结果,采用均方差作为距离计算。
注意:平均值距离差退化现象。采用平均值时,需要注意情报厂商数量减少到两家时的退化现象。当情报商数量仅有2家时,由于采用平均值作为最终评估结果,所以2个供应商与平均值的距离相等,采用距离公式进行评估的方法失效。
针对平均值模型的修正,对评价不一致的情报进行验证,采用验证结果比例进行权重分配进行修正。该修正方法引入了加权平均模型。
2.加权平均
采用加权平均算法时,需要注意的时,需要进行组合试算,寻找最小距离结果。
2.1.3家供应商(141分配),141分配来源于运筹学的经典公式,即悲观/乐观公式。
2.2.多家供应商(斐波那契数列),采用斐波那契数列和141公式有类似之处,权重采用的是经验值而非最佳值。采用经验数值的好处是避免了无限收敛运算,获得容忍阈值范围内的结果即可。
采用加权平均,可以应用蒙特卡洛模拟(Monte Carlo Simulation)寻求最小距离最优解。需要注意的是,最小距离不代表最佳质量。
以上两种方法,相对计算简单,对程序员的要求和算力要求都比较容易满足。接下来介绍的算法对程序员的数学基础和算力要求相对较高,这类算法广泛用于决策系统,对多目标决策和非确定性决策有着重要的意义。
在较为流行的开源威胁情报共享软件MISP中,也引用了加权平均的计算公式,如下图:
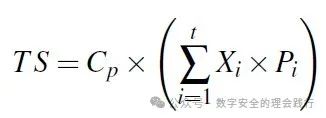
在公开的论文中(论文名称:Enriching Threat Intelligence Platforms Capabilities),作者提出了权重Cp选择的三个准则:1)与接受威胁情报的实体相关;2)实现业务价值;3)可操作,包括相关性、及时性、准确性、多样性、可摄性和完整性等,并约定不强制所有属性均加入加权计算。需要注意的是该公式采用了两个加权值,另一个维度Pi则使用类似于Delphi方法进行设定。同时,模型还提出了权重值需要进行训练和校准,但论文中并未给出训练和校准的具体公式。
以上数学模型,规则简单,对计算要求相对较低,易于实现。但对于评价差异不能良好的体现,并且无法表现出弃权(未给出评价)的信息。因此,在研究了更多的数学模型的应用,结合当前计算能力的发展。笔者认为针对威胁情报的数值表达,以及针对相应服务商的评价,可以采用具有更加丰富表达的模糊集和Vague集,模糊集的引入,还可以在一定程度上帮助解决历史数据不足和不够准确的局面。
3.模糊集
模糊集采用[0,1]之间的某个值作为威胁情报置信度的结果,因此比非黑即白能够表达更多的信息,该置信度中可以引入时间作为参数之一,使唯一的置信度结果值同时可以表达活跃度信息。由于模糊集的应用材料非常多,笔者不再赘述其应用。
4.Vague集
Vague集合引入了真隶属和假隶属两个表达式,用t(x)来表达真隶属,用f(x)表达假隶属。t(x) 从明确支持x的证据(黑名单)所导出的隶属上界, f(x)是从明确反对x的证据(白名单)所导出的否定隶属下界。t(x)+f(x)<=1。例如,在采用10个源进行威胁情报计算时,共有6家给出了明确的黑名单,1家给出了白名单,3家未给出信息,如果采用平均/加权平均等数学模型时,该结果将会被计算成唯一的数值进行表达,而在Vague集中,则被表达为[06,0.9],从该表达我们可以看出Vague用2个数值可以表达三个状态,0.6表示明确支持,0.1(1-0.9)表示明确否定,0.3(0.9-0.6)表示弃权。当t(x)+f(x)=1时,Vague集退化为模糊集。基于Vague集的TOPSIS(逼近理想值的排序技术)更是经常被IDS类产品用来作为威胁计算。基于Vague集的矩阵运算,则可以用来对威胁情报厂商进行评价。Vague集还支持多种距离算法(例如:欧氏空间距离,海明距离等),用来对模型自身进行优化。
对威胁情报和威胁情报厂商进行评价的数学模型,可以根据不同的场合进行选择,例如:目标精度要求、计算环境(算力)。希望以上的分享,能够广大威胁情报的从业者带来启发。
声明:本文来自数字安全的理会践行,版权归作者所有。文章内容仅代表作者独立观点,不代表安全内参立场,转载目的在于传递更多信息。如有侵权,请联系 anquanneican@163.com。
